Closed-form solution
To detect ellipse–circle collision (intersection or one being inside another), the point on the ellipse can be found from which a line perpendicular to the ellipse tangent at that point goes through the circle center. The point on the side closer to the circle center should be taken, not the point on the opposite side of the ellipse. If the point lies inside the circle, there is a collision. If the center of the circle is inside the ellipse, there is always a collision, and this should be tested for before making things more complicated. The same calculations could be used to detect any ellipse–ellipse collision by first using an affine transformation to stretch either of the ellipses into a circle; the other will remain an ellipse.
The closed form solution for the point on the ellipse is a gargantuan equation:
x = c*b^2/(2*(b^2 - 1)) - 1/2*sqrt(c^2*b^4/(b^2 - 1)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)/(3*(b^4 - 2*b^2 + 1)) - (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)/(b^2 - 1)^2 + (- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1) + sqrt((- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1))^2 - 4*(- 12*(b^4 - 2*b^2 + 1)*c^2*b^4 + 12*(b^4*c - b^2*c)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2)^3))^(1/3)/(3*2^(1/3)*(b^2 - 1)^2) + 2^(1/3)*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2/(3*(b^2 - 1)^2*(- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1) + sqrt((- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1))^2 - 4*(- 12*(b^4 - 2*b^2 + 1)*c^2*b^4 + 12*(b^4*c - b^2*c)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2)^3))^(1/3))) + 1/2*sqrt(2*c^2*b^4/(b^2 - 1)^2 - (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)/(3*(b^4 - 2*b^2 + 1)) - (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)/(b^2 - 1)^2 - (- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1) + sqrt((- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1))^2 - 4*(- 12*(b^4 - 2*b^2 + 1)*c^2*b^4 + 12*(b^4*c - b^2*c)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2)^3))^(1/3)/(3*2^(1/3)*(b^2 - 1)^2) - 2^(1/3)*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2/(3*(b^2 - 1)^2*(- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1) + sqrt((- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1))^2 - 4*(- 12*(b^4 - 2*b^2 + 1)*c^2*b^4 + 12*(b^4*c - b^2*c)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2)^3))^(1/3)) - (8*c^3*b^6/(b^2 - 1)^3 - 16*c*b^2/(b^2 - 1) - 8*c*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^2/(b^2 - 1)^3)/(4*sqrt(c^2*b^4/(b^2 - 1)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)/(3*(b^4 - 2*b^2 + 1)) - (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)/(b^2 - 1)^2 + (- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1) + sqrt((- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1))^2 - 4*(- 12*(b^4 - 2*b^2 + 1)*c^2*b^4 + 12*(b^4*c - b^2*c)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2)^3))^(1/3)/(3*2^(1/3)*(b^2 - 1)^2) + 2^(1/3)*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2/(3*(b^2 - 1)^2*(- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1) + sqrt((- 108*c^2*(b^4*c - b^2*c)^2*b^4 + 72*(b^4 - 2*b^2 + 1)*c^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)*b^4 + 2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^3 + 108*(b^4 - 2*b^2 + 1)*(b^4*c - b^2*c)^2 + 36*(b^4*c - b^2*c)^2*(c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1))^2 - 4*(- 12*(b^4 - 2*b^2 + 1)*c^2*b^4 + 12*(b^4*c - b^2*c)^2 + (c^2*b^4 - b^4 + d^2*b^2 + 2*b^2 - 1)^2)^3))^(1/3)))))
y = sqrt(1 - x^2)/b
In the equation, the ellipse is presumed to have a horizontal radius of 1 and to be centered at (0, 0), $b$ is the reciprocal of the vertical radius of the ellipse flipped such that $b\gt 1$, circle center is at $(c, d)$. Fortunately, the equation has reoccurring subexpressions and can be simplified using additional variables ($e$, $f$, $g$, $h$, $i$, $j$, $k$, $s$, $q$, $m$, $n$, $o$, $s3$, $p$, $s2$):
e = b^4*c^2 f = b^4 - 2*b^2 + 1 g = e - f + d^2*b^2 h = b^2*c i = b^2*h - h j = 72*f*e*g + 2*g^3 + (108*(f - e) + 36*g)*i^2 k = 12*i^2 + g^2 - 12*f*e s = j^2 - 4*k^3 q = (j + sqrt(s))^(1/3) m = b^2 - 1 n = 1/m o = g/(3*f) + g^2*n^2*2^(1/3)/(3*q) + (n^2*q*4^(1/3))/6 s3 = (e - g)*n^2 + o p = sqrt(s3) s2 = (2*e - g)*n^2 - o - (2*h*((e - g)*n^3 - 2/m))/p x = h/(2*m) - p/2 + sqrt(s2)/2 y = sqrt(1 - x^2)/b
Unfortunately, the implementation using limited floating point precision suffers from numerical instability and does not work for all mathematically valid input variable combinations. The highest power of $b$ in the expanded formula is 22, which is the likely cause of the instability. Combined with several early-out checks and other stability fixes, the formula appears to work. It has not been exhaustively tested, so stability is not guaranteed. You can try it out yourself below:
Usage: Drag to resize ellipse. A red dot indicates collision detected using the equation, and the circle and the ellipse turning red indicates collision detected by an early-out check.
Polygonal approximation
A circle can be sandwiched between an inscribed and a circumscribed regular polygon. If the other polygon is rotated by $\frac{\pi}{n}$, where $n$ is the number of corners in each polygon, then the two polygons meet at the corner points of the inscribed polygon, which coincide with the center point of each side of the circumscribed polygon. This forms triangles that enclose the rim of the circle in sections. If new inscribed and circumscribed polygons are drawn that have twice number of corners, then the triangles from these will be inside the old triangles and again enclose the rim of the circle.
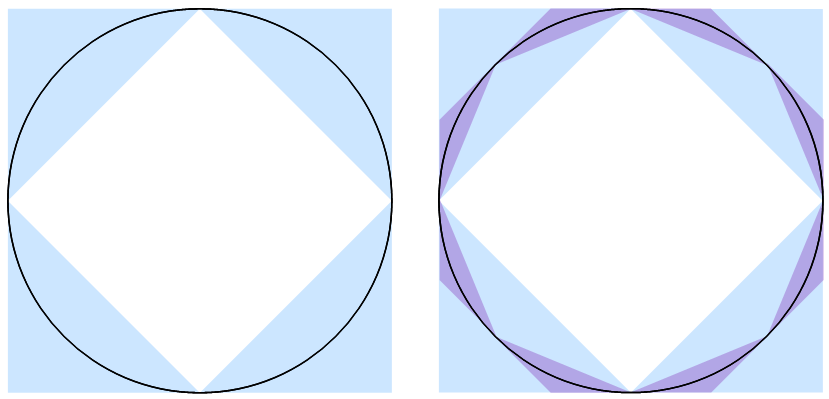
The same works for ellipses, by stretching the polygons along the axes of the ellipse. The triangles that enclose segments of the ellipse can be tested for collision with the circle. If the collision takes place at either of the corner points of the inscribed polygon or along the line segment that connects them, or if the ellipse center is inside the inscribed polygon, then the ellipse and circle have collided. If the collision takes place elsewhere in the triangle, then the triangle can be bisected into two smaller triangles, and the above checks can be repeated. Othewise, there is no collision.
So, one needs first a method to detect collisions of line segments and circles.
Line segment–circle collision detection
First, translate everything so that line start point is (0, 0). This is actually optional, but simplifies the expressions of the resulting coordinates. The translated coordinates are $(a, b)$ for the line segment end point and $(c, d)$ for the circle center, and $r$ is the circle radius. Then do a scaling and rotating transformation akin to complex multiplication:
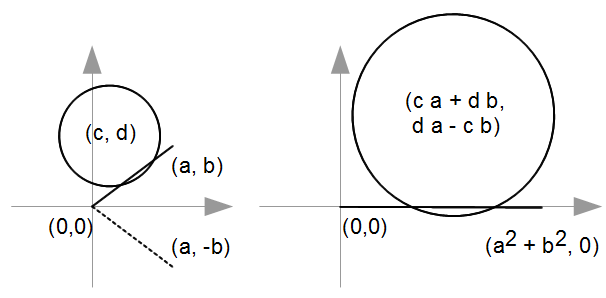
The scaling changes the circle radius from $r$ to $r \sqrt(a^2 + b^2)$, by the rules of complex multiplication. The sign of the new circle vertical coordinate, $d*a - c*b$, tells us on which side of the line the circle center resides. This is not needed for collision detection but may be useful information for something else, and it comes without extra cost as that term will be required anyhow. If the absolute value of the circle center vertical coordinate is greater than the radius, there can be no collision. The squares of those numbers can be more cheaply compared: There can only be a collision if $(da - cb)^2 \le r^2(a^2 + b^2)$, otherwise the algorithm terminates with a negative result. If either of the line segment end points is inside the circle, then there is a collision. This is easy to check for by comparing the squared circle radius to the squared distance between the circle center and each line segment end point: $c^2 + d^2 \le r^2$ for the start or $(a-c)^2 + (b-d)^2 \le r^2$ for the end indicates collision. If neither end point is inside the circle, the circle may still intersect with the middle part of the line segment. This is tested for by comparing the circle horizontal coordinate to the line segment end point coordinates. If the circle is in-between, then there is an intersection: $ca + db \ge 0$ and $ca + db \le a^2 + b^2$ must both be satisfied. Otherwise there is no collision, because that would already have been detected as either of the end points being inside the circle.
Usage: Drag to resize the line segment. Red indicates collision.
Ellipse–circle collision
The line segment–circle intersection test does not require the computation of a division or a square root; neither does an ellipse–circle collision test that employs it, using the enclosing triangle bisection scheme. The algorithm presented here is early-out in the sense that it does not calculate where exactly the collision took place, but terminates when it detects collision or as soon as the possibility of a collision vanishes. Usually, only one or two iterations (bisections) are needed. The algorithm could be modified to calculate also the intersection points, but this would require a great number of iterations in case of a collision. The following application demonstrates the algorithm.
Usage: Drag to resize the ellipse. Red indicates collision.
Approximation error
The maximum number of iterations in the algorithm can be limited to $n$. This gives a polygon with $2^{2+n}$ sides. The shortest distance between the ellipse and any point of the polygon is always less than $2^{0.303-2n}\text{max}(w, h)$, where $w$ and $h$ are the major and minor radii of the ellipse.
Ellipse–ellipse collision
Ellipse–ellipse collision test can be implemented using the polygonal ellipse-circle collision test after stretching of the ellipses so that the other becomes a circle. The calculation will be easier if the ellipses have parallel axes.
Parallel axes
If the axes are parallel (horizontal and vertical), it suffices to multiply all horizontal coordinates and horizontal radii by the vertical radius of the second ellipse, and all vertical coordinates and vertical radii by the (original) horizontal radius of the second ellipse. This makes the second ellipse a circle.
Non-parallel axes
If the ellipses do not have parallel axes, one could create a transformation matrix $A$ that does a rotation, stretching, and rotation back to make the second ellipse a circle and a rotation to align the major and minor axes of the first ellipse with the horizontal and vertical axes. Unfortunately, the equation needed in the last step for finding the major and minor axes of the first ellipse is very very complicated. It is better to only include the first three transformations in the matrix, and to transform the initial coordinates used in the polygonal algorithm using it. This suffices, because successive iterations of the algorithm use linear combination of coordinates to create coordinates for the smaller polygons; the properties of matrix multiplication are such that $A(aV + bW) = aAV + bAW$ where $A$ is a matrix, $a$ and $b$ are scalars, and $V$ and $W$ are vectors. An appropriate rotation–stretching–back-rotation matrix is:
$A = \left[\begin{array}{cc}hw1\ wx1^2 + wy1^2 & hw1\ wx1\ wy1 - wx1\ wy1\\ hw1\ wx1\ wy1 - wx1\ wy1& hw1\ wy1^2 + wx1^2\end{array}\right]$
where $(wx1, wy1)$ is the major or minor radius vector of the second ellipse and $hw1$ is the ratio between the other radius and that radius. The transformation of coordinates $(x, y)$ is done as:
$\left[\begin{array}{c}x\\ y\end{array}\right] \longmapsto A \left[\begin{array}{c}x\\ y\end{array}\right] = \left[\begin{array}{c}hw1\ wx1\ (wy1\ y + wx1\ x) - wy1\ (wx1\ y - wy1\ x)\\ hw1\ wy1\ (wy1\ y + wx1\ x) + wx1\ (wx1\ y - wy1\ x)\end{array}\right]$
The transformed squared radius of the second ellipse (now circle) is $hw1^2\ (wx1^2 + wy1^2)^3$. The polygonal algorithm can be modified so that it needs only the squared radius. Calculation of the square root is not necessary. The algorithm also remains free of the division operator.
Circle approximation
The segments circumscribing the ellipse in the polygonal algorithm could be replaced by circle segments. This would work at least in the case of ellipse–circle collision.
Source code
You can find the source code for the interactive visualizations written in the Processing language in my openprocessing.org portfolio, or by viewing the source code of this web page.
Ellipse–circle and Ellipse–ellipse collision test, polygonal approximation (C++)
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 |
#include <stdio.h> #include <math.h> /* Ellipse-circle collision detection * * by Olli Niemitalo in 2012-08-06. * This work is placed in the public domain. */ class EllipseCollisionTest { private: double *innerPolygonCoef; double *outerPolygonCoef; int maxIterations; bool iterate(double x, double y, double c0x, double c0y, double c2x, double c2y, double rr) const { for (int t = 1; t <= maxIterations; t++) { double c1x = (c0x + c2x)*innerPolygonCoef[t]; double c1y = (c0y + c2y)*innerPolygonCoef[t]; double tx = x - c1x; double ty = y - c1y; if (tx*tx + ty*ty <= rr) { return true; } double t2x = c2x - c1x; double t2y = c2y - c1y; if (tx*t2x + ty*t2y >= 0 && tx*t2x + ty*t2y <= t2x*t2x + t2y*t2y && (ty*t2x - tx*t2y >= 0 || rr*(t2x*t2x + t2y*t2y) >= (ty*t2x - tx*t2y)*(ty*t2x - tx*t2y))) { return true; } double t0x = c0x - c1x; double t0y = c0y - c1y; if (tx*t0x + ty*t0y >= 0 && tx*t0x + ty*t0y <= t0x*t0x + t0y*t0y && (ty*t0x - tx*t0y <= 0 || rr*(t0x*t0x + t0y*t0y) >= (ty*t0x - tx*t0y)*(ty*t0x - tx*t0y))) { return true; } double c3x = (c0x + c1x)*outerPolygonCoef[t]; double c3y = (c0y + c1y)*outerPolygonCoef[t]; if ((c3x-x)*(c3x-x) + (c3y-y)*(c3y-y) < rr) { c2x = c1x; c2y = c1y; continue; } double c4x = c1x - c3x + c1x; double c4y = c1y - c3y + c1y; if ((c4x-x)*(c4x-x) + (c4y-y)*(c4y-y) < rr) { c0x = c1x; c0y = c1y; continue; } double t3x = c3x - c1x; double t3y = c3y - c1y; if (ty*t3x - tx*t3y <= 0 || rr*(t3x*t3x + t3y*t3y) > (ty*t3x - tx*t3y)*(ty*t3x - tx*t3y)) { if (tx*t3x + ty*t3y > 0) { if (fabs(tx*t3x + ty*t3y) <= t3x*t3x + t3y*t3y || (x-c3x)*(c0x-c3x) + (y-c3y)*(c0y-c3y) >= 0) { c2x = c1x; c2y = c1y; continue; } } else if (-(tx*t3x + ty*t3y) <= t3x*t3x + t3y*t3y || (x-c4x)*(c2x-c4x) + (y-c4y)*(c2y-c4y) >= 0) { c0x = c1x; c0y = c1y; continue; } } return false; } return false; // Out of iterations so it is unsure if there was a collision. But have to return something. } public: // Test for collision between two ellipses, "0" and "1". Ellipse is at (x, y) with major or minor radius // vector (wx, wy) and the other major or minor radius perpendicular to that vector and hw times as long. bool collide(double x0, double y0, double wx0, double wy0, double hw0, double x1, double y1, double wx1, double wy1, double hw1) const { float rr = hw1*hw1*(wx1*wx1 + wy1*wy1)*(wx1*wx1 + wy1*wy1)*(wx1*wx1 + wy1*wy1); float x = hw1*wx1*(wy1*(y1 - y0) + wx1*(x1 - x0)) - wy1*(wx1*(y1 - y0) - wy1*(x1 - x0)); float y = hw1*wy1*(wy1*(y1 - y0) + wx1*(x1 - x0)) + wx1*(wx1*(y1 - y0) - wy1*(x1 - x0)); float temp = wx0; wx0 = hw1*wx1*(wy1*wy0 + wx1*wx0) - wy1*(wx1*wy0 - wy1*wx0); float temp2 = wy0; wy0 = hw1*wy1*(wy1*wy0 + wx1*temp) + wx1*(wx1*wy0 - wy1*temp); float hx0 = hw1*wx1*(wy1*(temp*hw0)-wx1*temp2*hw0)-wy1*(wx1*(temp*hw0)+wy1*temp2*hw0); float hy0 = hw1*wy1*(wy1*(temp*hw0)-wx1*temp2*hw0)+wx1*(wx1*(temp*hw0)+wy1*temp2*hw0); if (wx0*y - wy0*x < 0) { x = -x; y = -y; } if ((wx0 - x)*(wx0 - x) + (wy0 - y)*(wy0 - y) <= rr) { return true; } else if ((wx0 + x)*(wx0 + x) + (wy0 + y)*(wy0 + y) <= rr) { return true; } else if ((hx0 - x)*(hx0 - x) + (hy0 - y)*(hy0 - y) <= rr) { return true; } else if ((hx0 + x)*(hx0 + x) + (hy0 + y)*(hy0 + y) <= rr) { return true; } else if (x*(hy0 - wy0) + y*(wx0 - hx0) <= hy0*wx0 - hx0*wy0 && y*(wx0 + hx0) - x*(wy0 + hy0) <= hy0*wx0 - hx0*wy0) { return true; } else if (x*(wx0-hx0) - y*(hy0-wy0) > hx0*(wx0-hx0) - hy0*(hy0-wy0) && x*(wx0-hx0) - y*(hy0-wy0) < wx0*(wx0-hx0) - wy0*(hy0-wy0) && (x*(hy0-wy0) + y*(wx0-hx0) - hy0*wx0 + hx0*wy0)*(x*(hy0-wy0) + y*(wx0-hx0) - hy0*wx0 + hx0*wy0) <= rr*((wx0-hx0)*(wx0-hx0) + (wy0-hy0)*(wy0-hy0))) { return true; } else if (x*(wx0+hx0) + y*(wy0+hy0) > -wx0*(wx0+hx0) - wy0*(wy0+hy0) && x*(wx0+hx0) + y*(wy0+hy0) < hx0*(wx0+hx0) + hy0*(wy0+hy0) && (y*(wx0+hx0) - x*(wy0+hy0) - hy0*wx0 + hx0*wy0)*(y*(wx0+hx0) - x*(wy0+hy0) - hy0*wx0 + hx0*wy0) <= rr*((wx0+hx0)*(wx0+hx0) + (wy0+hy0)*(wy0+hy0))) { return true; } else { if ((hx0-wx0 - x)*(hx0-wx0 - x) + (hy0-wy0 - y)*(hy0-wy0 - y) <= rr) { return iterate(x, y, hx0, hy0, -wx0, -wy0, rr); } else if ((hx0+wx0 - x)*(hx0+wx0 - x) + (hy0+wy0 - y)*(hy0+wy0 - y) <= rr) { return iterate(x, y, wx0, wy0, hx0, hy0, rr); } else if ((wx0-hx0 - x)*(wx0-hx0 - x) + (wy0-hy0 - y)*(wy0-hy0 - y) <= rr) { return iterate(x, y, -hx0, -hy0, wx0, wy0, rr); } else if ((-wx0-hx0 - x)*(-wx0-hx0 - x) + (-wy0-hy0 - y)*(-wy0-hy0 - y) <= rr) { return iterate(x, y, -wx0, -wy0, -hx0, -hy0, rr); } else if (wx0*y - wy0*x < wx0*hy0 - wy0*hx0 && fabs(hx0*y - hy0*x) < hy0*wx0 - hx0*wy0) { if (hx0*y - hy0*x > 0) { return iterate(x, y, hx0, hy0, -wx0, -wy0, rr); } return iterate(x, y, wx0, wy0, hx0, hy0, rr); } else if (wx0*x + wy0*y > wx0*(hx0-wx0) + wy0*(hy0-wy0) && wx0*x + wy0*y < wx0*(hx0+wx0) + wy0*(hy0+wy0) && (wx0*y - wy0*x - hy0*wx0 + hx0*wy0)*(wx0*y - wy0*x - hy0*wx0 + hx0*wy0) < rr*(wx0*wx0 + wy0*wy0)) { if (wx0*x + wy0*y > wx0*hx0 + wy0*hy0) { return iterate(x, y, wx0, wy0, hx0, hy0, rr); } return iterate(x, y, hx0, hy0, -wx0, -wy0, rr); } else { if (hx0*y - hy0*x < 0) { x = -x; y = -y; } if (hx0*x + hy0*y > -hx0*(wx0+hx0) - hy0*(wy0+hy0) && hx0*x + hy0*y < hx0*(hx0-wx0) + hy0*(hy0-wy0) && (hx0*y - hy0*x - hy0*wx0 + hx0*wy0)*(hx0*y - hy0*x - hy0*wx0 + hx0*wy0) < rr*(hx0*hx0 + hy0*hy0)) { if (hx0*x + hy0*y > -hx0*wx0 - hy0*wy0) { return iterate(x, y, hx0, hy0, -wx0, -wy0, rr); } return iterate(x, y, -wx0, -wy0, -hx0, -hy0, rr); } return false; } } } // Test for collision between an ellipse of horizontal radius w0 and vertical radius h0 at (x0, y0) and // an ellipse of horizontal radius w1 and vertical radius h1 at (x1, y1) bool collide(double x0, double y0, double w0, double h0, double x1, double y1, double w1, double h1) const { double x = fabs(x1 - x0)*h1; double y = fabs(y1 - y0)*w1; w0 *= h1; h0 *= w1; double r = w1*h1; if (x*x + (h0 - y)*(h0 - y) <= r*r || (w0 - x)*(w0 - x) + y*y <= r*r || x*h0 + y*w0 <= w0*h0 || ((x*h0 + y*w0 - w0*h0)*(x*h0 + y*w0 - w0*h0) <= r*r*(w0*w0 + h0*h0) && x*w0 - y*h0 >= -h0*h0 && x*w0 - y*h0 <= w0*w0)) { return true; } else { if ((x-w0)*(x-w0) + (y-h0)*(y-h0) <= r*r || (x <= w0 && y - r <= h0) || (y <= h0 && x - r <= w0)) { return iterate(x, y, w0, 0, 0, h0, r*r); } return false; } } // Test for collision between an ellipse of horizontal radius w and vertical radius h at (x0, y0) and // a circle of radius r at (x1, y1) bool collide(double x0, double y0, double w, double h, double x1, double y1, double r) const { double x = fabs(x1 - x0); double y = fabs(y1 - y0); if (x*x + (h - y)*(h - y) <= r*r || (w - x)*(w - x) + y*y <= r*r || x*h + y*w <= w*h || ((x*h + y*w - w*h)*(x*h + y*w - w*h) <= r*r*(w*w + h*h) && x*w - y*h >= -h*h && x*w - y*h <= w*w)) { return true; } else { if ((x-w)*(x-w) + (y-h)*(y-h) <= r*r || (x <= w && y - r <= h) || (y <= h && x - r <= w)) { return iterate(x, y, w, 0, 0, h, r*r); } return false; } } EllipseCollisionTest(int maxIterations) { this->maxIterations = maxIterations; innerPolygonCoef = new double[maxIterations+1]; outerPolygonCoef = new double[maxIterations+1]; for (int t = 0; t <= maxIterations; t++) { int numNodes = 4 << t; innerPolygonCoef[t] = 0.5/cos(4*acos(0.0)/numNodes); outerPolygonCoef[t] = 0.5/(cos(2*acos(0.0)/numNodes)*cos(2*acos(0.0)/numNodes)); } } ~EllipseCollisionTest() { delete[] innerPolygonCoef; delete[] outerPolygonCoef; } }; int main(int argc, const char **argv) { EllipseCollisionTest test(10); { double x0 = -1.0; double y0 = 5.0; double w = 10; double h = 20; double x1 = 25; double y1 = 7; double r = 15; printf("Ellipse:\nCenter: (%f, %f)\nHorizontal radius: %f\nVertical radius: %f\n\n", x0, y0, w, h); printf("Circle:\nCenter: (%f, %f)\nRadius %f,\n\nResult: ", x1, y1, r); if (test.collide(x0, y0, w, h, x1, y1, r)) { printf("Collision.\n"); } else { printf("No Collision\n"); } } printf("---\n"); { double x0 = -10.0; double y0 = 5.0; double wx0 = 10.0; double wy0 = 20.0; double hw0 = 3.0; double x1 = 3.0; double y1 = 4.0; double wx1 = 5.0; double wy1 = -4.0; double hw1 = 0.75; printf("First ellipse:\nCenter: (%f, %f)\nFirst radius vector: (%f, %f)\nRatio between second and first radius: %f \n\n", x0, y0, wx0, wy0, hw0); printf("Second ellipse:\nCenter: (%f, %f)\nFirst radius vector: (%f, %f)\nRatio between second and first radius: %f \n\nResult: ", x1, y1, wx1, wy1, hw1); if (test.collide(x0, y0, wx0, wy0, hw0, x1, y1, wx1, wy1, hw1)) { printf("Collision.\n"); } else { printf("No Collision\n"); } } } |

The problem can be formulated as an eigenvalue problem to achieve an efficient numerical algorithm. Also, you may find this interesting: http://books.google.fi/books?id=8CGj9_ZlFKoC&pg=PA72&lpg=PA72&dq=hill+conic+sections+graphics+gems&source=bl&ots=yAgrQD0rBF&sig=C0lOQy5NHp0ybs1uZU40QJbWkig&hl=en&sa=X&ei=PRHTUfPhJ-bx4QT7oIGICA&redir_esc=y#v=onepage&q=hill%20conic%20sections%20graphics%20gems&f=false
sm, can you tell more about the eigenvalue-based algorithm?
Something here:
@article{ROB:80017,
author = {Ju,Ming-Yi and Ju,Ming-Yi and Liu,Jing-Sin and Shiang,Shen-Po and Chien,Yuh-Ren and Hwang,Kao-Shing and Lee,Wan-Chi },
title = {Fast and accurate collision detection based on enclosed ellipsoid},
journal = {Robotica},
volume = {19},
issue = {04},
month = {7},
year = {2001},
issn = {1469-8668},
pages = {381–394},
numpages = {14},
doi = {10.1017/S0263574700003295},
URL = {http://journals.cambridge.org/article_S0263574700003295},
}
http://www.iis.sinica.edu.tw/papers/liu/637-F.pdf
@MISC{Rimon97obstaclecollision,
author = {Elon Rimon and Stephen P. Boyd},
title = { Obstacle Collision Detection Using Best Ellipsoid Fit},
year = {1997}
}
https://www.stanford.edu/~boyd/papers/pdf/obst-coll-det.pdf