2010-03-05
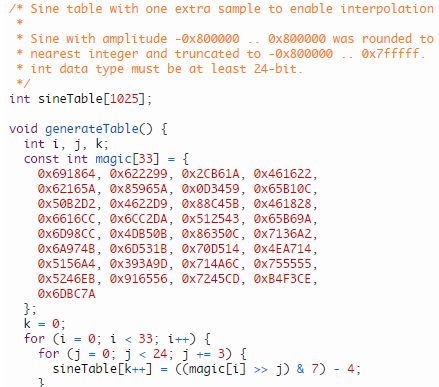
Here is a method for generating a sine look-up table in case you have little (a few kilobytes of) program memory. The idea goes like this: Let's say you have a sine wave lookup table of length 1024 with a 24-bit amplitude range. If you take the difference between successive samples, the range of the numbers is reduced. If you repeat the process a total of 3 times, the data will be dominated by the 3rd differential of the quantization noise and will have a range of -4 to 3, which can be conveniently stored in 3 bits only. This program below does the reverse, it generates the sine table from the 3-bit values, and also takes advantage of the symmetry properties of sine. So, instead of wasting 1024 program memory words for storing the original sine table, in the c-language implementation below, the compressed data takes only 35 24-bit words and the decompression code hopefully not too much more.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
/* Multiplierless 1024-sample, 24-bit sine table generator * * by Olli Niemitalo in 2010-03-07. * This work is placed in the public domain. */ #include <stdio.h>; /* Sine table with one extra sample to enable interpolation * * Sine with amplitude -0x800000 .. 0x800000 was rounded to * nearest integer and truncated to -0x800000 .. 0x7fffff. * int data type must be at least 24-bit. */ int sineTable[1025]; void generateTable() { int i, j, k; const int magic[33] = { 0x691864, 0x622299, 0x2CB61A, 0x461622, 0x62165A, 0x85965A, 0x0D3459, 0x65B10C, 0x50B2D2, 0x4622D9, 0x88C45B, 0x461828, 0x6616CC, 0x6CC2DA, 0x512543, 0x65B69A, 0x6D98CC, 0x4DB50B, 0x86350C, 0x7136A2, 0x6A974B, 0x6D531B, 0x70D514, 0x4EA714, 0x5156A4, 0x393A9D, 0x714A6C, 0x755555, 0x5246EB, 0x916556, 0x7245CD, 0xB4F3CE, 0x6DBC7A }; k = 0; for (i = 0; i < 33; i++) { for (j = 0; j < 24; j += 3) { sineTable[k++] = ((magic[i] >> j) & 7) - 4; } } sineTable[1] = 51472; for (i = 3; i > 0; i--) { for (j = i; j <= 256; j++) { k = sineTable[j - 1]; sineTable[j] = k + sineTable[j]; sineTable[513-j] = k; sineTable[511+j] = -k; sineTable[1025-j] = -k; } } sineTable[768] = -0x800000; } int main() { int i; generateTable(); /* Printout */ for (i = 0; i < 1025; i++) { printf("%d\t%d\n", i, sineTable[i]); } return 0; } |
Here is a spreadsheet that illustrates the algorithm: sinetable.xls. The above implementation additionally embeds the seeds 0 and -3 in the magic data
Very nice!
Why are you using 24-bit words, when they’ll almost always be stored as 32-bit integers? Surely you could save another 25% by using the high byte of each word as well?
Matthew: I used a processor with 24-bit program memory words when I wrote this. Yeah someone could write a 32-bit version…
I have another solution. You know how you can approximate the cosine/sine using polynomials? And how every time you halve the range your polynomial covers you multiply the precision by 2^(degree of the polynomial + 1)? So you got your x = [0, 2^32-1] input that represents the angle in turns, do the symmetry thing to turn it into a value in the first quadrant, take the top N bits, use them as the index for your array of polynomial coefficients, compute the polynomial by doing (((c2 * xl >> fmt) + c1) * xl >> fmt) + c0; (for quadratic approximations), change the sign depending on the input quadrant, and there’s your result!
If you go with quadratic approximations and 32 segments then you only need a 384 byte pre-computed table (32 segments, 3 coefficients per segment, coefficients are 32 bits) and you get max error of 1/1,450,000 (-123 dB), and on a modern computer it runs in about 15 cycles (I don’t use symmetry so it goes even faster). You can save more memory using a smaller table (at the cost of a max of 8x precision for each 2x decrement) or using higher degree polynomials (at the expense of CPU time).
Michel, I believe your performance figures, they sound very plausible. Here’s more on using polynomials for sin cos generation: http://www.rossbencina.com/code/sinusoids
Hello
Can you advise how to make 2 channels , DAC , Sine wave look-up table for 14.kHz with resolution 1mV for STM32T100 ?
Hallo
How I can use this table to produce 15 kHz sine wave ?
ted:
1/ generate a sinewave from the code
2/ play the sinewave through an audio device at a high enough sample rate to complete each cycle within 1/15000th of a second
Assuming the output of this code is a full wave cycle (rather than the quarter wave used in e.g. the Yamaha OPL lookup tables), you’ll need to replay at about 15.36MHz.
Obviously it’s only really worth doing this if you need to generate a signal for technical reasons rather than for audio. The ear can’t really determine between different wave shapes at that high a frequency (because what the ear actually picks up is the harmonic overtones caused by different timbres, rather than the wave shape itself, and any overtones for sounds above about 12kHz are inaudible to most people). In that case you’ll be more than well served by simply producing a repeating pattern of 0, +1, 0, -1 and replaying it at 60kHz, or even just +1, -1 replayed at 30kHz.
If you want it to be aliased into a waveform of more standard frequency (say 32, 44.1 or 48kHz) then your best bet is to load up an audio editor such as Audacity that offers fundamental waveform generation and ask it to brew you up a 15kHz sine.
Or go through the table at a different speed and use linear interpolation. There’s one extra sample at the end to facilitate this.