Marginal notes

These are miscellaneous notes and recipes.

Mapping a pair of integers to an integer

2011-05-26

How to map from a pair of integers to an integer? Negative or positive, independent of the size of the two integers, you can convert them into balanced ternary to get rid of the signs and then interleave the digits starting from the least significant digits. Pad with leading zeros if the other integer is longer.

When working with non-negative numbers or on a fixed binary bit depth, interleaving bits works fine (see Z-order curve).

Logarithm of a sum of large numbers

2010-03-30

When dealing with large numbers, it can be useful, as an approximation, not to deal with the numbers themselves, but with their logarithms. This has the added benefit that multiplication of two numbers corresponds to taking the sum of their logarithms. But what if you want to take the sum of the numbers, $a$ and $b$, how can you avoid dealing with the possibly horrendously large numbers themselves? This problem may be encountered for example when computing the total unnormalized probability (a Boltzmann factor or partition function) of mutually exclusive events. Here's a way:

Presume that $a>0$, $b>0$, and $a \ge b$. If $a < b$ you can always swap the two numbers.

$\mathrm{ln}(a + b) = \mathrm{ln}\big(a(1+\frac{b}{a})\big) = \mathrm{ln}\,a + \mathrm{ln}(1+\frac{b}{a}) = \mathrm{ln}\, a + \mathrm{ln}\big(1 + \mathrm{e{x}p}(\mathrm{ln}\,b - \mathrm{ln}\,a)\big) $.

If $\mathrm{ln}\,b - \mathrm{ln}\,a$ is a very large negative number, then $\mathrm{ln}(a + b) \approx \mathrm{ln}\,a$.

For the logarithm of the difference of $a$ and $b$, we would proceed similarly:

Presume that $a>0$, $b>0$, and $a > b$. These conditions are necessarily satisfied if $\mathrm{log}\,a$, $\mathrm{log}\,b$, and $\mathrm{log}(a - b)$ can be calculated.

$\mathrm{ln}(a - b) = \mathrm{ln}\big(a(1-\frac{b}{a})\big) = \mathrm{ln}\,a + \mathrm{ln}(1-\frac{b}{a}) = \mathrm{ln}\, a + \mathrm{ln}\big(1 - \mathrm{e{x}p}(\mathrm{ln}\,b - \mathrm{ln}\,a)\big) $.

If $\mathrm{ln}\,b - \mathrm{ln}\,a$ is a very large negative number, then $\mathrm{ln}(a - b) \approx \mathrm{ln}\,a$.

$\mathrm{ln}\big(1 + \mathrm{e{x}p}(x)\big)$ and $\mathrm{ln}\big(1 - \mathrm{e{x}p}(x)\big)$  are called Gaussian logarithms, because Carl Friedrich Gauss was the first to publish printed tables of them.

One application for a Gaussian logarithm is in calculation of the transition energy to a state from its complement state that covers the remainder of the phase space or thermodynamic ensemble. When the Boltzmann factor of the state and the partition function of the system are known, but both expressed as energy ($E_{\mathrm{state}}$ and $E_{\mathrm{system}}$, respectively), the calculation for the transition energy $E_{\mathrm{transition}}$ turns out as: $E_{\mathrm{transition}} = E_{\mathrm{state}} - E_{\mathrm{system}} - k_{\beta} T\ \mathrm{ln}\big(1-\mathrm{e{x}p}(-\frac{E_{\mathrm{state}} - E_{\mathrm{system}}}{k_{\beta}T})\big)$, where $k_{\beta}$ is the Boltzmann constant and T is temperature. The transition the other way would simply change the sign of the transition energy.

Newbie bug with C++ nested templates

2010-03-02

Say, you want to create a map from stings to vectors of strings. Why does this (with the appropriate STL includes):

typedef std::vector VectorOfStrings; typedef std::map StringToVectorOfStrings;

1	typedef std::vector VectorOfStrings; typedef std::map StringToVectorOfStrings;

work, while this doesn't:

typedef std::map&gt; StringToVectorOfStrings;

1	typedef std::map> StringToVectorOfStrings;

The latter works if you modify it a little bit, so that the consecutive >'s are not recognized as >>:

typedef std::map &gt; StringToVectorOfStrings;

1	typedef std::map > StringToVectorOfStrings;

Two IRC channels in different windows using EPIC IRC client

2009-10-15

Start your IRC session like this:

/window new /window show 1 /bind ^I parse_command {/window size 6} {/window last} {/window move 1}

1 2 3

/window new /window show 1 /bind ^I parse_command {/window size 6} {/window last} {/window move 1}

Now you have two windows on top of each other, and you are doing things in the bottom one. You can switch between the windows by pressing tab.

The normal usage is to join on two different channels:

/join #firstchannel

1	/join #firstchannel

Press tab.

/join #secondchannel

1	/join #secondchannel

Whenever you want to view or talk on the other channel, press tab.

Embedding a Java Applet in a WordPress 2.8.4 post (also works in 3.2.1)

2009-09-12

In the HTML editor:

<div id="dyemixer">APPLET HERE<script type="text/javascript">// <![CDATA[ document.getElementById('dyemixer').innerHTML = '<applet width="550" height="420" code="DyeMixer.class" archive="http://yehar.com/blog/wp-content/uploads/2009/09/DyeMixer.jar" alt="To use this applet, you need a Java virtual machine (Java plug-in) for your web browser.">'; // ]]></script></div>

This also survives editing the post in the visual editor. You can even center the applet like you would a normal paragraph.  Note that the div's id and the argument to getElementById must be identical. Using a similar JavaScript script, you should be able to put also other arbitrary HTML in a WordPress post or page.

Generation of random numbers from a truncated exponential distribution

2009-07-30

To generate a random number with a truncated exponential distribution:

1. Generate a random number $x$ from an exponential distribution with the rate parameter you want
2. Calculate $x$ modulo where-to-truncate. This would not be integer modulo but for example fmod() floating-point remainder.

Could be useful if you have exponentially distributed random numbers handy.

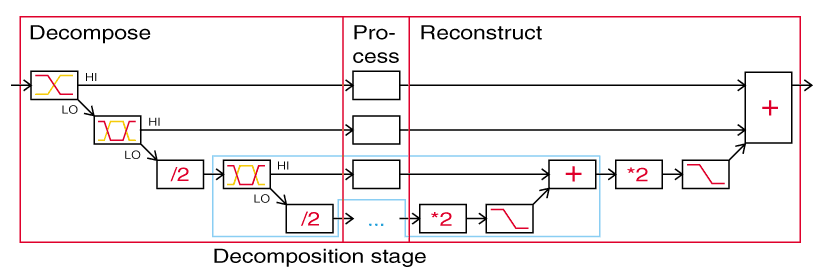
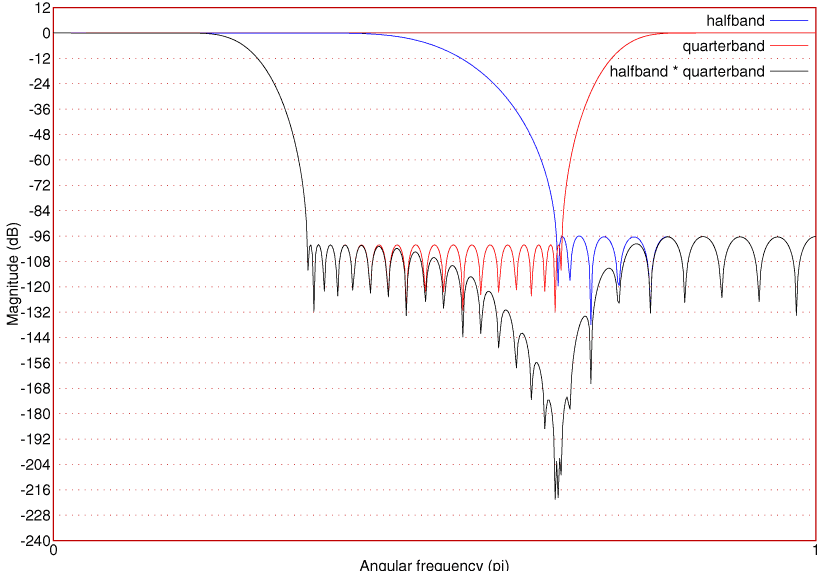
Anti-imaged wavelet transform

2002-11-25

This is an idea of a wavelet-type audio processing scheme, where you decompose the audio into octave bands, each octave sampled at half the sampling frequency compared to the one-up octave band. Then you process the bands in whatever way you wish, and reconstruct the signal from the bands. The benefit of the method compared to usual wavelets is the low level of imaging noise when bands are processed separately. The original music-dsp posting has the details:

http://aulos.calarts.edu/pipermail/music-dsp/2002-November/018600.html

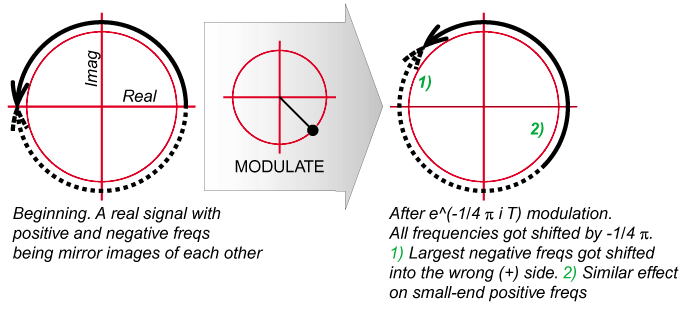
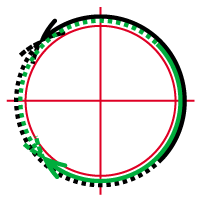
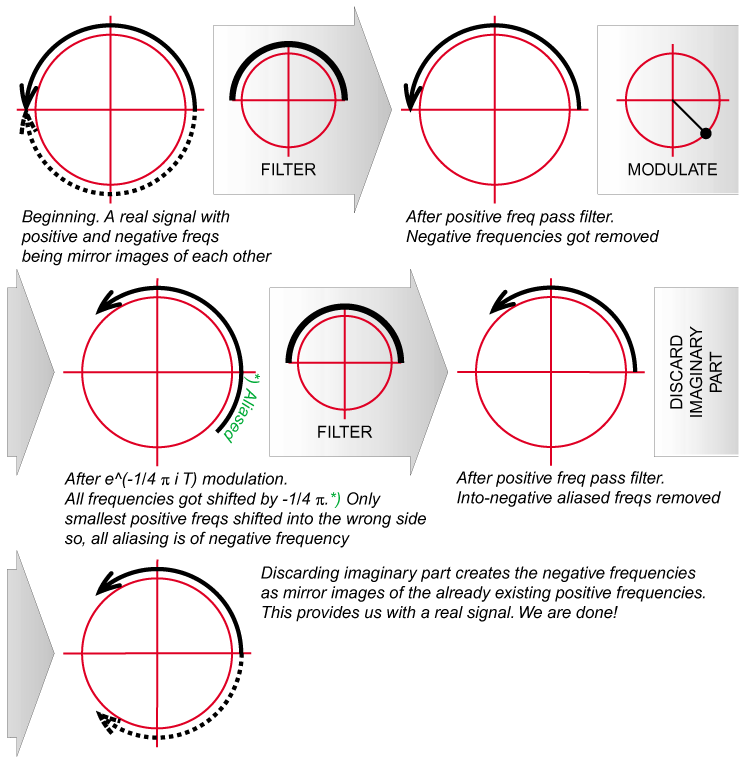
Frequency shifting (audio effect)

2001-09-02

Frequency shifting can be an interesting audio effect, although it does not usually preserve harmonic relations. Here is how to do it the wrong and the right way:

Daubechies wavelets 1-38 in a .h file

2000-08-10

I copied some daubechies wavelets from a published database into this C header file, confirmed the data to be error-free and wrote a little introduction into wavelets in the comments.