I am interested in an enumeration of functions that starts with simple functions and progresses to more computationally expensive functions. Such an enumeration would enable to systematically try all useful functions for some task. For efficiency, it would be nice if the enumeration did not contain duplicate copies of the same function. Further, because the same function can be produced by multiple algorithms, for example $((a + b) + b)$ vs. $((b + b) + a)$, it would be nice to avoid also such semantic duplicates. The best would be if only the simplest algorithm giving each function would be in the enumeration.
Polynomials
A side step on the way to more general algorithms is polynomials. Here is a list of all polynomials with (your choice) integer or rational coefficients, optionally including negative coefficients. It is a long list as you will find out by scrolling. As a bonus, the index can be Gray coded to make successive polynomials differ only at one power of $x$. This makes their evaluation in the order of the enumeration faster.
|
You can jump to anywhere on the list as it is not generated recursively but is directly evaluated at any given value of the index. The construction of the enumeration uses the Stern–Brocot tree for integer-to-rational conversion and the following integer sequences from the Online Encyclopedia of Integer Sequences (OEIS):



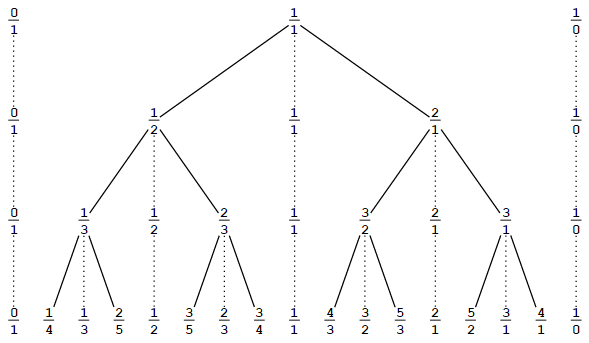
In the integer-to-rational conversion, the most significant set bit of the integer is found and the less significant bits decide which rational number tree branches are taken. If the integer is signed, the resulting rational number inherits its sign and only the absolute value is converted.
For interleaving of bits I also tried the ruler function A001511 but to my taste it gave too large coefficients for the smallest powers of $x$, relative to the higher powers. At the limit of large numbers, the currently used sequence A002260 allocates an equal proportion of bits to different powers of $x$.
The enumeration is valid: no two polynomials in the enumeration are equal, and any polynomial will be in the list if its coefficients are in the chosen set of numbers. But this is only one of infinitely many valid enumerations. Just as an example, using or not using the Gray code results in two different enumerations that are both valid. The choice of the rational number tree has a similar effect.
Sorting by complexity
The above list of polynomials is not sorted by increasing algorithmic complexity. For example $1 - 2x + x^2 = (1+x)^2$ is found later on the list than the irreducible polynomial $1 + x + x^2 = 1 + (1 + x)x$, which is slower to calculate in a fully sequential multiply-add-subtract integer computer. In a computer with infinitely many parallel units they both evaluate in 2 steps. Another pair of polynomials, one irreducible, is enumerated in the wrong order also for the infinitely parallel computer: $1 + 4x + 6x^2 + 4x^3 + x^4 = ((1+x)^2)^2$ and $1 + x + x^2 + x^3 + x^4$. The enumeration seems quite oblivious of any internal structure of the polynomials that can be used to speed up computations.
An enumeration that sorts the polynomials in increasing order of multiply-add-subtract steps is impossible. At the first level of such an ordering would be numerical constants and $x$ itself. There is an endless number of the constants so we would never see any polynomials requiring one or more steps. Skipping the first level completely we would only encounter the same problem at the second level, and so on. One solution would be to penalize also for the magnitude of constants, but this would neglect the likely fact that structured numbers (such as $255 = 2^{2^3}-1$) are more useful in algorithms than other numbers. But how should such structure be defined? Perhaps by forcing the function to generate its own numerical constants from simple basic components such as the numbers 0 and 1, by computation. A problem is that some efficient algorithms such as Fast Fourier Transform make use of irrational numbers even for rational inputs and outputs, and it may be that equal performance cannot be matched by rational-only algorithms. Similarly, if there is fast division available, it could also speed up computation of powers such as $x^{31} =xx(xx)\left(xx(xx)\right)\left[xx(xx)\left(xx(xx)\right)\right]\left\{xx(xx)\left(xx(xx)\right)\left[xx(xx)\left(xx(xx)\right)\right]\right\}/x$.
