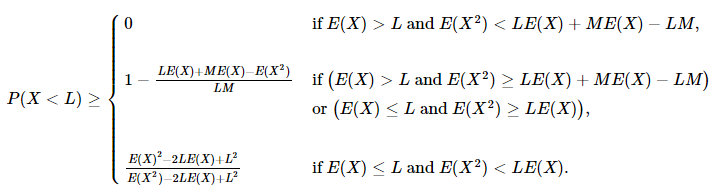2007-12-14
Chebyshev's inequality states that, for any probability distribution, at most $1/k^2$ of the area of the probability density function lies more than $k$ standard deviations away from the mean. We can do better, if we know that the distribution is bounded and we know the bounds.

Let $X$ be a random variable bounded by $0 \le X \le M$, where $M > 0$. Given the first two moments, $E(X)$ and $E(X^2)$, of its probability distribution, a sharp lower bound to $P(X <L)$, where $L > 0$, is given by:

$$P(X < L)\ge \left\{ \begin{array}{ll} 0 & \mbox{if $E(X) > L$ and $E(X^2) < L E(X) + M E(X) - L M$,}\\\\ 1 - \frac{L E(X) + M E(X) - E(X^2)}{L M} & \mbox{if $\big (E(X) > L$ and $E(X^2) \ge L E(X) + M E(X) - L M \big )$}\\ & \mbox{or $\big(E(X) \le L$ and $E(X^2) \ge L E(X)\big)$,}\\\\ \frac{E(X)^2 - 2 L E(X) + L^2}{E(X^2) - 2 L E(X) + L^2} & \mbox{if $E(X) \le L$ and $E(X^2) < L E(X)$.} \end{array} \right.$$

That's it. On a related note...

Let $X$ be a random variable and $L$ a constant both bounded by $0 \le X \le M$ and $0 \le L \le M$, where $M > 0$.

Let $Y$ be a random variable otherwise equal to $X$, but collecting the tail of $X$ exceeding $L$ to $L$:

$$Y = \left\{\begin{array}{ll} X & \mbox{if $X \le L$,} \\ L & \mbox{if $X > L$.}\\ \end{array}\right.$$

$E(Y)$ and $E(Y^2)$ cannot be determined knowing only $E(X)$, $E(X^2)$, $M$ and $L$. However, sharp upper bounds to $E(Y)$ and $E(Y^2)$ are given by:

$$\begin{array}{c} E(Y) \le \left\{ \begin{array}{ll} L & \mbox{if $E(X) > L$ and $E(X^2) < L E(X) + M E(X) - L M$,} \\\\ \frac{LE(X)+ME(X)-E(X^2)}{M} & \mbox{if $\big(E(X) > L$ and $E(X^2) \ge L E(X) + M E(X) - L M\big)$ or} \\ & \mbox{$\big(E(X) \le L$ and $E(X^2) \ge L E(X)\big)$,} \\\\ E(X) & \mbox{if $E(X) \le L$ and $E(X^2) < L E(X)$,} \end{array}\right.\\\\ E(Y^2) \le \left\{ \begin{array}{ll} L^2 & \mbox{if $E(X) > L$ and $E(X^2) < L E(X) + M E(X) - L M$,} \\\\ \frac{L^2E(X)+LME(X)-LE(X^2)}{M} & \mbox{if $\big(E(X) > L$ and $E(X^2) \ge L E(X) + M E(X) - L M\big)$ or} \\ & \mbox{$\big(E(X) \le L$ and $E(X^2) \ge L E(X)\big)$,} \\\\ E(X^2) & \mbox{if $E(X) \le L$ and $E(X^2) < L E(X)$.} \end{array}\right. \end{array}$$

Beats me how to prove these formulas, but I tried with tens of thousands of randomly generated distributions and they always worked. The way I got the formulas was by trying to think of the "worst-case" distributions (that's why these are sharp bounds). There were a few of these, corresponding to the different conditions. So I think I know the worst cases, but I don't know how to show that these truly are the worst cases.

Henry Bottomley has written more about Chebyshev type inequalities.